on
论文阅读|图上的自监督学习——对比学习论文解读
前言
本文将围绕最近的一些在图上自监督学习的工作,对其中“Contrastive Learning”的内容进行一些解读,并包括一些自监督学习的思路。
首先,介绍一篇2020的综述《Self-supervised Learning: Generative or Contrastive》,其内容覆盖了CV、NLP、Graph三个方向自监督学习的成果。而本文会将主要目光放在Graph上的自监督学习。
文章将自监督学习主要分为三类:Generative、Contrastive、Adversarial(Generative-Contrastive)。目前,个人认为大部分Graph研究的目光都集中在Contrstive Learning上。个人拙见,原因可能与图学习的任务有关,图学习的任务主要集中在分类上(节点分类、图分类),对比学习天然会比生成学习更适用于分类任务,所以或许当生成满足某种性质的随机图任务成为主流之后,生成式模型就会成为主流。而对抗式(Adversarial)的学习,则会在生成式学习、对比式学习都达到瓶颈时,得到更好的发展。目前,在图领域,并未看到Adversarial Learning有惊人表现的文章。
当笔者初识自监督学习时,通过他人的介绍,仅理解为了一种利用自身性质,标注更多标签的一种手段,但随着论文阅读的增加,对自监督本质的理解越来越迷惑。个人理解,其实任意挖掘对象之间联系、探索不同对象共同本质的方法,都或多或少算是自监督学习的思想。原始的监督学习、无监督学习,都被目所能及的一切所约束住,无法泛化,导致任务效果无法提升,正是因为自监督探索的是更本质的联系,而不是表像的结果,所以其效果通常出乎意料的好。自监督学习的前两类方法,其核心想法其实都是想去探索事物的本质。
本文重点将放在Contrastive Learning的发展脉络上,对于Generative Learning将只结合《Self-supervised Learning: Generative or Contrastive》介绍一些粗浅的理解。
Generative Self-Supervised Learning
综述中主要介绍了四类基于生成式的自监督模型,最后一类是前三类模型的混合版,而在图学习领域,使用的比较多的应该是第三种,即AE的方法,在后文总结表格中有所体现,这里也就不对混合型生成模型进行描述了。
Auto-Regressive (AR) Model
文章提到 “自回归模型可以看作是贝叶斯网络结构”。Auto-Regressive Model 最初是在统计上处理时间序列的方法,时间序列最基础的两种模型就是AR与MA。AR的理论基础确实就是贝叶斯方法,也就是条件概率的一套理论。任意一个节点的分布都可以借其他节点作为条件,以此计算自身的概率分布。这样的思想用在图生成和扩张上,再适合不过。线性回归是最基础的预测模型,预测的结果就是生成的目标。
Flow-based Model
flow-based models 是希望估计数据的复杂高维分布。这个方法也可以找到和统计相关的方法。思想其实是广义线性回归模型,都是想用一个潜变量对未知的复杂分布进行估计。
Auto-Encoding (AE) Model
Auto-Encoder Model 有点像主成分分析方法,其原理是将原有的输入映射到一个新的维度,再将其映射回原来的维度。类似于主成分的方法,这样的操作需要保证映射的目标需要保持某些性质(相似度高的节点,映射后应该相似性依然高),同时这个过程可以降噪。这也是一个非常值得研究的方向。
Contrastive Self-Supervised Learning
此综述提及,最近因为在自监督学习方向有几项工作有所突破,这些工作都集中在对比学习上,很大程度上说明当前研究的重心主要偏向对比式的自监督学习。这些突破性的工作主要有Deep InfoMax、MoCo、SimCLR。
对比学习最初是想通过Noise Contrastive Estimation(NCE)学习目标对象之间的差别。目标对象之间的区别其实就是相似程度,相似程度是一个比较主观的概念,其实是同任务有关的。通常我们说的挖掘信息,就是在增加衡量相似程度的指标。笔者所接触的最早衡量两个节点相似程度的方法是DeepWalk,从一个节点所能到其他节点的概率,这就是它的相似性。训练这类模型的方法通常有两种,一种是通过定义损失函数,并采样正负例使损失函数最小,另一种方法是直接求解损失函数的极值,通过矩阵分解的方式求最优解。由此,NCE的核心其实是在损失函数,即:
\[\mathcal{L}=\mathbb{E}_{x,x^+,x^k}[-\log(\frac{ e^{f(x)^\top f(x^+) } }{ e^{f(x)^\top f(x^+)}+\sum_{k=1}^K e^{f(x)^\top f(x^k)} } )]\] 所谓图上的对比学习,其实就是对于任意两个节点,若越相似(属于同一类)其图表示就会越接近,什么样的节点作为正例/负例,就决定了最后分类的效果。
由于这个损失的分母是比较难计算的,特别是随着负例的增加。之前的方法通常是使用它的等价形式进行训练,即使用Skip-Gram with Negative Sampling(SGNS):
\[\mathcal{L}=\log\sigma(f(x)^\top f(x^+))+k\mathbb{E}_{x^-\sim P_N}[\log\sigma(-f(x)^\top f(x^-))]\] \[\sigma \ is \ sigmoid \ function\]而Deep InfoMax 则是在NCE的基础上,走出了另一个道路,其目标为:
\[\underset{\omega_{1}, \omega_{2}, \psi}{\arg \max }\left(\alpha \widehat{\mathcal{I}}_{\omega_{1}, \psi}\left(X ; E_{\psi}(X)\right)+\frac{\beta}{M^{2}} \sum_{i=1}^{M^{2}} \widehat{\mathcal{I}}_{\omega_{2}, \psi}\left(X^{(i)} ; E_{\psi}(X)\right)\right)+{\arg \min _{\psi} \arg \max_{\phi} } \gamma \widehat{\mathcal{D}}_{\phi}\left(\mathbb{V} \| \mathbb{U}_{\psi, \mathbb{P}}\right)\] 对这个目标函数意义感兴趣的可以直接阅读原文,这里主要关注图学习,所以主要说明它对图上自监督学习的启示。对接Deep InfoMax的工作主要是Deep Graph InfoMax(DGI)。Deep InfoMax主要的启示是利用局部和全局互信息。DGI使用的还是GCN的框架,通过利用readout function得到对节点的一个表示,这里利用了全局信息,再通过构造负例(对应节点的特征重排,再与拓扑结构信息结合),使生成的节点表示更接近正例(对应节点的拓扑结构信息和特征的结合)。由于每次的负例都需要重排特征,这样的生成负例方式是非常耗时的,所以DGI使用了mini batch。
其实图上许多方法都是从其他领域套用而来,并取得了很多比较好的效果,特别是NLP中的文本就可以看作是一种特殊的图。下面将谈一些基于其他方向,转化到图学习的一些成果。
Contrastive Multi-View Representation Learning on Graphs
《Contrastive Multi-View Representation Learning on Graphs》是一篇ICML2020的文章。他在GCN的三个数据集中都达到了很高的效果。聊这篇论文,可以先分析他的思想来源,弄清思想来源其实是进一步工作的灵感,无中生有的idea其实是非常不容易的,大部分工作还是提出一点改进和迁移现有的工作。
Multi-View其实是在DGI的基础上,对全局和局部互信息进行了新的扩展。他的依据主要是《Learning Representations by Maximizing Mutual Information Across Views》中所提出的对DIM的改进方法:Augmented Multi-scale DIM (AMDIM)。这篇文章提出可以用不同的增强数据的方式,定义局部和全局的互信息损失。在DIM是一个视图生成的“Real”和“Fake”之间的对比,而在AMDIM则是在不同增强视图之间“Real”和“Fake”之间的对比,也就是更好地利用全局信息。
所谓Multi-View在图像上是各种图片增强的方式,MVRLG则提出将ADJ、PPR、Heat Kernel看作Graph不同的Multi-View。他的核心代码其实就是DGI的代码,区别在于定义了两个GCN,每个GCN对应一种View,衡量正负例的区别时,通过交换正例在不同View下的结果,同交换负例在不同View下的结果,协同训练节点的embedding,同时也可以生成Graph的表示,进行Graph Classification。 以下为Multi-View提出的模型,从左侧开始,定义不同的diffusion(ADJ、PPR、Heat Kernel),并在diffusion上进行采样,并借用DGI的框架,构造两个GNN。通过对特征的重排,生成负例。交换两个GNN的输入,即文章提到的共享MLP,将一个diffusion下的输入作为另一个GNN的输入,再与交换的负例进行对比学习。
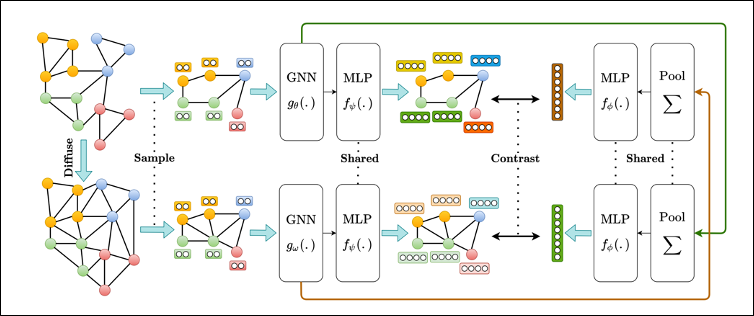
这篇文章虽然叫Multi-View,但其实还是在两个View之间进行的实验,论文中有提到,将View增加之后的效果有可能会变差。根据图像的发展思路,在两个View之间进行对比学习必然还是可以扩展的。《Contrastive Multiview Coding》就是认为同一个物体有多种视角(不同的数据增强方式,理论上是无限多的),这篇文章就是希望能够综合多个视角下的信息,对数据进行训练。
GCC: Graph Contrastive Coding for Graph Neural Network Pre-Training
在图上一样有 follow CMC的工作,比如同样是唐杰老师组的一篇论文《GCC: Graph Contrastive Coding for Graph Neural Network Pre-Training》。值得一提的是,这篇文章其实也描述了一种图上View的形式,而且与前一篇文章有异曲同工之妙。首先,GCC定义了子图实例,借用Random Walk with Restart 从r-ego网络中,针对某个节点,导出正例子图,并将其他节点通过此方式导出的子图作为负例。
下图为论文使用的例子,左侧的红色节点为输入节点。以某一节点进行r层的广度搜索所生成的图即为r-ego network。在r-ego network的限制下,从输入节点做RWR,可以生成一系列的子图,这些子图可以作为正例。从其他节点在r-ego network做RWR,生成的一系列子图则可以当作是负例。
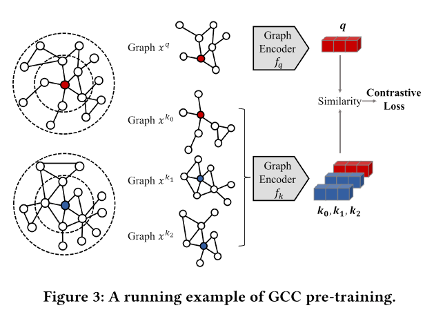
在《Are Graph Convolutional Networks Fully Exploiting Graph Structure? 》一文中,讨论了RWR与1WL-test有密切的关系。事实上,说两种利用Multi-View做自监督学习的共通之处就在于,RWR本质上就是PPR。原因很简单,每进行深一层的随机游走有一定的概率回到原始节点,而回去的概率是成比例递增的,往下一层走的概率也就成比例递减,并按度均匀分配到邻居节点上,这正是PPR。所以这里导出的子图的分布其实是与节点的PPR分布密切相关的。GCC是一种Pre-Trainning方法,后续使用什么样的GCN Models其实并不是很关键,只需要生成足够多的正负例,类似于图片的训练,输入到GCN中进行训练即可,原文用的是GIN。
同样的,在图上做自监督学习一样会面临着负例不足的问题,这篇文章利用了自监督学习最新的成果MoCo。MoCo的优点在于不用梯度更新负例的参数,而是用“Momentum“,即用正例参数去更新负例,但需要将这部分的更新控制得非常小。SimCLR和MoCo都是想要解决负例数量的问题,这点倒是与什么领域关系不大,所以利用这些成果是非常自然的事。
对于以上的自监督学习,《Self-supervised Learning: Generative or Contrastive》给出了很好的总结表格,以下摘抄了其中对图自监督学习的部分,并对Multi-View进行了补充,如下表:
| Model | Type | Generator | Self-supervision | Pretext Task | Hard NS | Hard PS | NS strategy |
|---|---|---|---|---|---|---|---|
| DeepWalk-based | G | AE | Graph Edges | Link Prediction | F | F | E2E |
| VGAE | G | AE | Graph Edges | Link Prediction | F | F | E2E |
| DGI | C | - | Context-instance | MI Max. | T | F | E2E |
| InfoGraph | C | - | Context-instance | MI Max. | F | F | E2E(batch-wise) |
| $S^2GRL$ | C | - | Node attributes | MI Max. Masked attribute prediction | F | F | E2E |
| GCC | C | - | Context-Context | instance discrimination | F | T | Momentum |
| ANE | G-C | AE | Graph Edges | Link Prediction | - | - | - |
| GraphGAN | G-C | AE | Graph Edges | Link Prediction | - | - | - |
| GraphSGAN | G-C | AE | Graph nodes | Node Classification | - | - | - |
| MVRLG | C | - | Context-instance | MI Max. | T | F | E2E |
未来可能的工作
目前在自监督方向可以做的图神经网络学习的内容还是比较多的,MoCo已经用于GCC中,那么在MVRLG中是否能使用呢?而MVRLG在多于两个GCN的效果就会下降,这背后的原因又是什么呢?目前看起来,图自监督学习的大部分结果都是由图像上的理论的提出而推进的,什么数据结构在这个领域其实并不特别重要,但自监督的思想是十分重要的。最后,当前的自监督学习始终还是面临无法将规模做大的问题,例如MVRLG要求每个epoch都将特征打乱,再计算PPR乘特征向量,其实消耗的时间还是挺大的,改进负例的构成尤为必要。
参考文献
[1] Liu, X. , Zhang, F. , Hou, Z. , Wang, Z. , Mian, L. , & Zhang, J. , et al. (2020). Self-supervised learning: generative or contrastive.
[2] Hassani, K. , & Khasahmadi, A. H. . (2020). Contrastive multi-view representation learning on graphs.
[3] Qiu, J. , Chen, Q. , Dong, Y. , Zhang, J. , & Tang, J. . (2020). Gcc: graph contrastive coding for graph neural network pre-training.
[4] Velikovi, P. , Fedus, W. , Hamilton, W. L. , Liò, Pietro, Bengio, Y. , & Hjelm, R. D. . (2018). Deep graph infomax.
[5] Tian, Y. , Krishnan, D. , & Isola, P. . (2019). Contrastive multiview coding.
[6] Hjelm, R. D. , Fedorov, A. , Lavoie-Marchildon, S. , Grewal, K. , Bachman, P. , & Trischler, A. , et al. (2018). Learning deep representations by mutual information estimation and maximization.
[7] P. Bachman, R. D. Hjelm, and W. Buchwalter. Learning represen- tations by maximizing mutual information across views. In NIPS, pages 15509–15519, 2019.