Written by
冥郡
on
on
空间多维数据展示--涟漪图
1. 研究问题
1.1研究问题背景
多年来,全国雾霾爆发,在地理空间上是否存在规律?2017年全国数学建模大赛提出给“拍照赚钱”任务定价,数据是否在位置上呈现一些规律?越来越多的研究定位在空间数据之上。
多维数据存在着展示上不直观的特点,数据容易“纠缠在一起”,想看出数据的变化规律、空间分布规律存在一定的障碍,通常人们将多维数据投影到二维上,但数据的“纠缠”仍然是比较难解决的,而展示多维数据的变化规律需要有一种能动态变化可视化手段。在看到水滴产生的涟漪、画画时颜色的相互交融时,突发灵感,提出一种新的可视化图——涟漪图。
1.2研究问题说明
多维分类型数据,分类的展示可以用点图轻松展示,但无法体现出多维分类数据的每一个分类的紧密程度,哪些分类间存在着“纠缠”,以及数据变化的主要方向。总的来说,多维数据是不能简单用每个维度的均值来衡量的,于是需要一种动态化展示的方法。
1.3数据说明
本次作业为了降低采集数据成本,使用2017年全国数学建模大赛的部分数据集,但制作涟漪图的核心在于中心点如何选取,目前采用的是kmeans方法,选取核心点,所以核心数据仅剩下两部分,经度、维度。对任意数据集,都可以使用二维投射,将点放置到二位图像中。
2. 方法介绍
2.1涟漪图说明
空间数据存在着重心,从kmeans出发,在聚类之后,数据有着一个核心的中点,借着这个核心的中点,可以在一定规则下画一组曲线集,从例子来说,在空间上确定中心后,可以从中心向外不断扩散,选定步长以后画椭圆,而椭圆实际是有方向的,可以将长轴看作是一个方向,确定中心和方向的椭圆,只再需要两个点即可确定其图形,同时新画的椭圆是可以包含原椭圆的。从另一个中心发射出的椭圆,会与原来的中心的椭圆相交,这样很可能产生新的颜色,这也就和涟漪一样,故我命名其为涟漪图。
2.2算法说明
算法如下:
1. 根据kmeans将数据分类(如果数据本身有分类,其实不需要这一步)
2. 以kmeans确定的中心C,将数据集按照到中心的距离进行排序,按升序排列
3. 选定步长为k,k为每次画椭圆包含进来的点的个数,设i=1
4. 以C为中心,设距离C最近的ik个点中最远的点为A,以|AC|为半长轴,CA的方向为长轴方向,绘制最小的能包含这ik个点的椭圆。
5. i=i+1, 重复步骤4,直到所有点都被椭圆覆盖
2.3算法实现
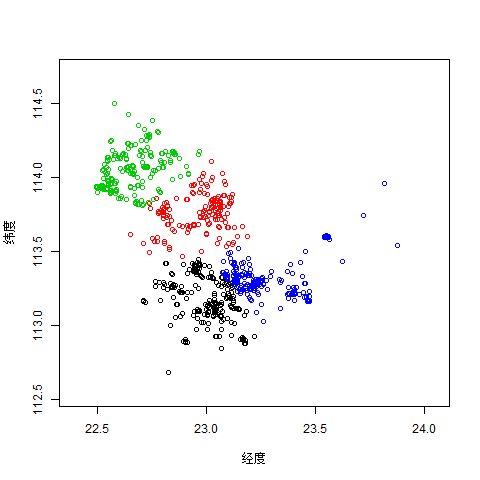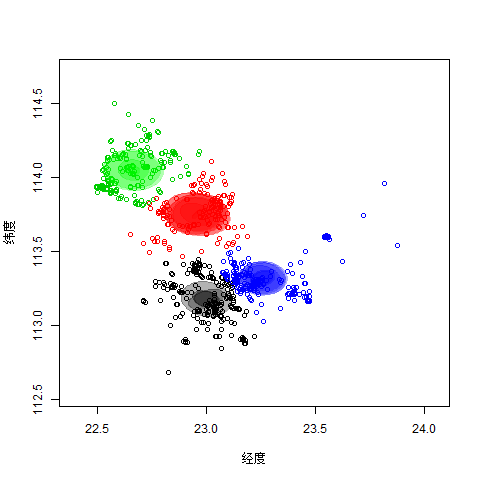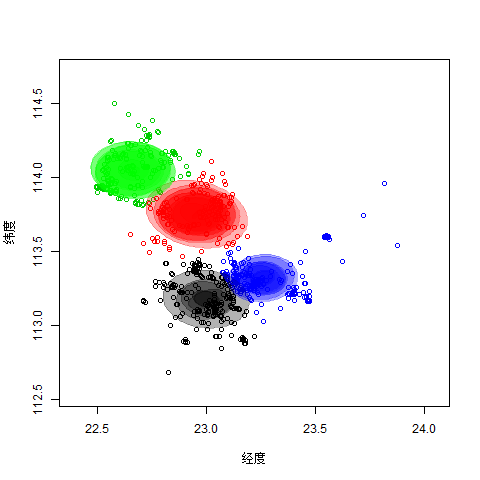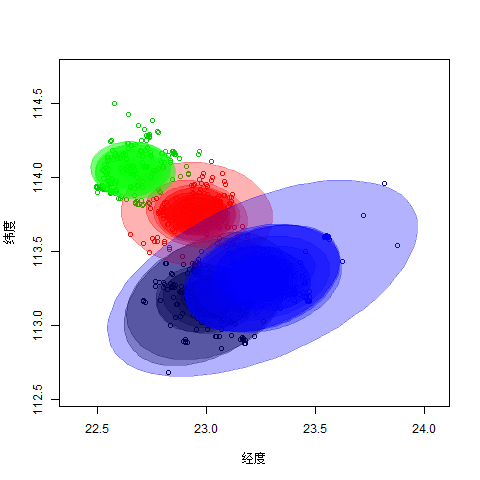
2.4图片描述分析
1. 目前将数据分作4组,从空间上看,每组数据都从经度方向扩散比较严重,也就是说可能经度是一个比纬度更为重要的一个因素。
2. 从分类的散度上,也能看出几个层次,在前期的数据中,绿色与红色扩散的比较快,但蓝色、黑色稍慢,后期则是蓝色扩散比较快,那么有可能是蓝色这个分类还需要进一步划分。
3. 从数据的纠缠上看,蓝色与黑色的数据“纠缠”比较严重,这和相关性应该是不一样的,可能是两者之间存在一些联系。反之,绿色与红色虽然在一个方向,但“泾渭分明”,可以从一定层次上说明两者就属于两个不同的类别,可借鉴的相似点少
3.方法分析
3.1 与其他方法的对比
3.1.1 涟漪图的优势
(1).可扩展性,相较于现在的涟漪使用的是椭圆,但类似于五角星、三角形、心形线、logo等等更多曲线,只要定义了画图方式,都能做出新的涟漪图。同时目前定义的椭圆长轴方向也可以根据如主成分方向等等做出符合使用者目的的调整。
(2).直观,涟漪始终是在动态下最佳,虽然制作动画有一定难度,但从数据展示层面,动画能最好的体现出数据之间的分散程度、中心的位置、数据空间上的变化趋势。
(3).展现数据的重叠性,在设计这个图的伊始,我并未想起等高线图,在突然想起等高线图后,产生了对自我创新的怀疑后,突然意识到等高线图也未必就比涟漪要更好,这种创新恰恰能做到等高线做不到的事。在数据重叠的部分,登高线图形成鞍部,但在涟漪图里表现出来的缺失动态性的数据之间的倾轧,它能更好地表现出数据的趋势,这是一层层画等高线是完全不一样的两种想法,等高线图需要一层层切开去看,是从上往下的,而实际数据的本质应该是一层层堆积出来的,假设有三类数据的层叠,根据颜色的配比,涟漪会更好的展示出底层的数据有多少是来自于那一类,但显然等高线图是做不到的。
3.1.2 涟漪图的不足
(1).绘制的困难,涟漪图毕竟还未成熟,在改变参数或者基础元素使需要考虑在空间中做什么样的变化,这也是需要不断完善的。
(2).选择中心点过多时,由于颜色混杂,导致视觉效果展示不出来。
4. 总结
从涟漪图的构造过程中,可以很好地对比两个维度数据之间拉锯地关系。但实际数据研究中,该方法是不是有效,还需要实践地不断检验。
5. 参考文献
无
6. 附录
library(animation)
library(jpeg)
library(plotrix)
three_point_oval<-function(center,long_point,pointset,col){
#三点画椭圆
distance<-function(a,b){return(sqrt((a[1]-b[1])^2+(a[2]-b[2])^2))}
cout_minor_axis<-function(center,aim,dis){
return(min( sqrt( (aim[1]-center[1])^2/(1-(aim[2]-center[2])^2/dis^2) ),sqrt( (aim[2]-center[2])^2/(1-(aim[1]-center[1])^2/dis^2) ) ))
}
rotate<-function(vec,center,mat){
return((vec-center)%*%mat+center)
}
point<-function(vec){
points(x=vec[1],y=vec[2])
}
direction_matrix<-1/2*sqrt((long_point[1]-center[1])^2+
(long_point[2]-center[2])^2)*matrix(c(1/(long_point[1]-center[1]),
1/(long_point[1]-center[1]),1/(long_point[2]-center[2]),
-1/(long_point[2]-center[2])),nrow=2,ncol=2,byrow=T)
#计算出旋转矩阵
rotate_set<-t(apply(pointset,1,rotate,center=center,mat=direction_matrix))
major_axis_dis<-distance(center,long_point)
minor_axis_dis<-max(apply(rotate_set,1,cout_minor_axis,center=center,dis=major_axis_dis))
draw.ellipse(center[1],center[2],major_axis_dis,minor_axis_dis,col=col,angle=(atan((long_point[1]-center[1])/(long_point[2]-center[2])))*180/pi,border=col)
#point(center)
#point(long_point)
#apply(pointset,1,point)
}
plot(x=1.2*(dat$任务gps.纬度-median(dat$任务gps.纬度))+rep(median(dat$任务gps.纬度),length(dat[,1])),y=(dat$任务gps经度-median(dat$任务gps经度))*1.2+rep(median(dat$任务gps经度),length(dat[,1])),type="n")
#将坐标扩充
da<-as.matrix(cbind(c(dat$任务gps.纬度),c(dat$任务gps经度)))
km<-kmeans(da,4)
set.seed(345)
for(j in 1:4){
new_da<-da[which(km$cluster==j),]
ds<-apply(new_da,1,distance,b=km$centers[j,])
nda<-new_da[order(ds,decreasing=F),]
col=rgb(runif(1,0,255),runif(1,0,255),runif(1,0,255),40,maxColorValue = 255)
for(i in seq(1,length(nda[,1]),3)){
three_point_oval(km$centers[j,],nda[i,],as.matrix(nda[1:i,]),col)
}
}
points(da,col=km$cluster)
saveGIF({#动画
ani.options(interval=0.2,nmax=1000,ani.width=1024,ani.height=1024,
convert = shQuote('C://Program Files (x86)/ImageMagick-6.2.7-Q16/convert.exe'))
minlen=c(length(which(km$cluster==1)),length(which(km$cluster==2)),length(which(km$cluster==3)),length(which(km$cluster==4)))
set.seed(345)
#col=rbind(c(runif(1,0,255),runif(1,0,255),runif(1,0,255),40,maxColorValue = 255),
# c(runif(1,0,255),runif(1,0,255),runif(1,0,255),40,maxColorValue = 255),
# c(runif(1,0,255),runif(1,0,255),runif(1,0,255),40,maxColorValue = 255),
# c(runif(1,0,255),runif(1,0,255),runif(1,0,255),40,maxColorValue = 255))
#随机颜色版本
col=rbind(c(0,0,0),
c(1,0,0),
c(0,1,0),
c(0,0,1))
for(i in seq(1,max(minlen),6)){
plot(x=1.2*(dat$任务gps.纬度-median(dat$任务gps.纬度))+rep(median(dat$任务gps.纬度),length(dat[,1])),y=(dat$任务gps经度-median(dat$任务gps经度))*1.2+rep(median(dat$任务gps经度),length(dat[,1])),type="n",xlab="经度",ylab="纬度")
points(dat,col=dat$任务标价)
for(j in 1:4){
templen=min(minlen[j],i)
new_da<-da[which(km$cluster==j),]
ds<-apply(new_da,1,distance,b=km$centers[j,])
nda<-new_da[order(ds,decreasing=F),]
colo=rgb(col[j,1],col[j,2],col[j,3],alpha = 0.3)
for(k in seq(1,templen,3)){
three_point_oval(km$centers[j,],nda[k,],as.matrix(nda[1:k,]),colo)
}
}
ani.pause()
}
})