Written by
冥郡
on
on
“神抽”还是“鬼抽”?炉石发牌员偏好探究
背景介绍
《炉石传说》是一款集换式卡牌游戏,玩家根据自己现有的卡牌组建合适的卡组,驱动随从,施展法术,与对手一决高下。而作为一款卡牌游戏,除了自身收藏卡牌之外,取得胜负最为关键的一点在于,关键时候是否能抽到关键的卡牌。不少玩家吐槽炉石传说可能存在一个发牌员,为了增加玩家的游戏时间,对发牌机制做了控制,以达到鬼抽/神抽的目的。而实际上,炉石暗地里调整各种选牌概率也不是第一次了。例如:著名的竞技场11只剑龙骑术,极大的降低了玩家的用户体验。
笔者学习《实验设计》课程中,便希望能利用上课知识,为了验证网络上一直以来对发牌员偏好的猜测,开始了简单的实验。研究游戏动态过程过于复杂,所以以起手发牌换牌为例,完成一次简单的探究——炉石中的起手发牌规律。

一、实验设计
1.数据说明,为了探究抽牌上手的因素,将因变量确定为以下几类:
| 名称 | 数据记作 | 备注 |
|---|---|---|
| “上手卡牌顺序” | 记为”次序” | 标识每次实验中,抽到的卡牌 |
| “法力水晶费用” | 记为”费用” | 取值为0-9+ |
| “卡牌稀有度” | 记为”稀有度” | 取值为0-3,对应白卡/蓝卡/紫卡/橙卡(卡牌稀有度越高,越难收集,若暴雪公司需要盈利,迎合”人民币玩家”,稀有卡牌的上手率可能会高) |
| “是否为职业卡牌” | 记为”职卡” | 取值为0/1,1为是职业卡牌 |
| “法术或随从” | 记为”法随” | 取值为0/1,1为随从牌,0为法术牌 |
| “初始手牌或二次手牌” | 记为”牌次” | 取值为0/1,1为初始手牌,2为更换手牌后的手牌,这里是为了验证更换手牌是否能得到更好的结果。 |
2. 实验总体说明,炉石卡牌很多,但每次游戏仅能携带30张卡牌,所以为了方便实验,构造了一个卡组尽量满足均匀设计,进行实验。实验卡牌说明如下:
| 变量 | 类型 | 30张卡牌中各类型张数 | 其他说明 |
|---|---|---|---|
| 费用 | 0-9 | 每个费用各三张 | 对战起始费用是1,每个回合能拥有的费用+1,上限是10 |
| 稀有度 | 白/蓝/紫/橙 | 8/8/7/7 | 因为橙卡比较难得到 |
| 职卡 | 职业/非职业 | 15/15 | 职业一般更强 |
| 法随 | 法术/随从 | 10/20 | 法术比较少,大部分是随从,所以比例定为1:2 |
| 牌次 | 首次/二次 | 1:1 | 每次将初始手牌更换,得到更换手牌数据 |
3. 实验流程说明
1. 利用构造好的实验卡组,在2018年4月1日,连续开始对局55局,并认输(仅测试起手抽牌)。
2. 人工记录每次对局开始时,上手的卡牌的详细情况,为防止出现错记情况,李某、刘某两人同时开始记录,并核对数据。
3. 测试时,仅用一个炉石账号进行比较,防止由于用户之间存在区别对待带来的差异。
二、数据分析
1.描述统计
实际游戏中,起手换不换牌是一个博弈的过程,而为了增加“天胡”的可能性,如何换牌,是一个值得探究的内容,所以借着下面一副简单的直方图和概率密度图像,验证一下心中的疑惑,以及为“发牌员”的喜好因素做一个简单的探索。
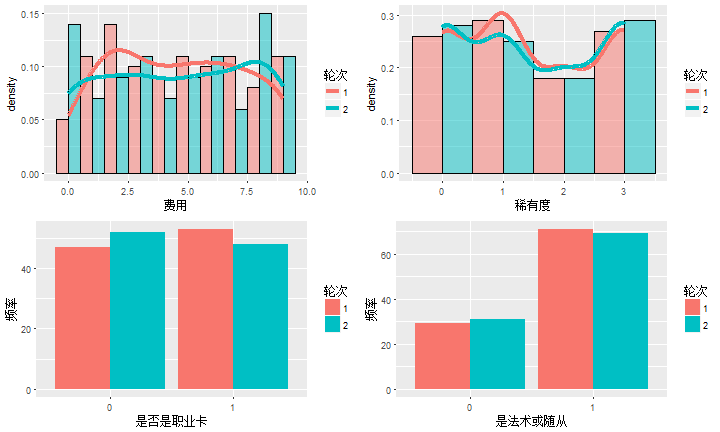
图1. 不同轮次,不同因素上手次数图 左上记为图1.1,右上记为图1.2,左下记为图1.3,右下记为图1.4
a.根据图1.1可以发现,换不换牌存在区别,换牌之后费用会稍高一些,也就是说当起始手牌适中时,希望搏一搏,换更小的点数手牌时,“发牌员”可能会给你更糟糕的牌,但是不是整体上2次选牌费用会变高还需要进一步检验。
b.根据图1.2发现,本应该8:8:7:7的概率分布图并不是心理预期的比例,“橙卡”是否真的容易“上手”,需要进一步检验,但橙卡容易被抽到,的确更能增加玩家的兴趣。
c.根据图1.3换卡似乎更能将非职业卡换到手上,但实际两者对比差别并不大,也并不特别影响游戏的平衡,“发牌员”是不是职业卡并不是很有兴趣
d.卡组法术:随从=1:2,但从图1.4手时,法术:随从=3:7,两者存在差别,但发牌员是否对“随从”情有独钟,仍需要进一步检验。
2.非参数检验
\(\chi^2\) 检验
a.检验整体来说,上手的费用是不是均匀的
$$ H_0: 均匀 vs H_1: 不均匀 $$
##
## Chi-squared test for given probabilities
##
## data: table(dat$费用)
## X-squared = 2.7, df = 9, p-value = 0.975
没有足够把握认为能拒绝原假设,认为上手费用是均匀的
b.检验先后次序不同,是否对费用产生影响
$$ H_0 :先后费用频次来自同一总体 vs H_1 :先后费用不来自一个总体 $$
##
## Pearson's Chi-squared test
##
## data: first and second
## X-squared = 32.5, df = 25, p-value = 0.144
没有90%的把握认为先后次序会对费用产生影响,无法拒绝原假设
c.检验卡牌稀有度是否会影响上手概率
$$ H_0:卡牌稀有度不会影响上手概率 vs H_1:卡牌稀有度会影响上手概率 $$
##
## Chi-squared test for given probabilities
##
## data: table(dat$稀有度)
## X-squared = 5.28, df = 3, p-value = 0.1524
没有90%的把握认为卡牌稀有度会影响上手概率,无法拒绝原假设
binom检验
a.简单探究交互作用 玩家通常还比较关注的一个点是,强力低费橙卡是否特别容易上手,所以对低费橙卡的上手率也做一个简单的检验
$$ H_0:低费橙卡上手概率 = \frac{1}{30} vs H_1:低费橙卡上手概率\neq\frac{1}{30} $$
##
## Exact binomial test
##
## data: length(d[, 1]) and 200
## number of successes = 7, number of trials = 200, p-value = 0.8426
## alternative hypothesis: true probability of success is not equal to 0.03333333
## 95 percent confidence interval:
## 0.01418553 0.07078100
## sample estimates:
## probability of success
## 0.035
无法拒绝原假设,证明类似于“二王子贼”这样的强大“天胡”卡组,每次核心牌在手上的概率并没有被调整过,实际上,这与赌徒心态特别类似,少量的赢钱给了玩家每次都能赢钱的暗示,但实际上,这样一张橙卡起手就在手上的概率才3%,但低费将其拍出的概率则更高,这也就验证了每套卡组仅能带一张橙卡的合理性。
b.验证是否随从比法术更容易上手
$$H_0:随从上手率=\frac{1}{3} vs H_1:随从上手率\neq\frac{1}{3}$$
##
## Exact binomial test
##
## data: sum(dat$法随) and 200
## number of successes = 140, number of trials = 200, p-value =
## 0.3305
## alternative hypothesis: true probability of success is not equal to 0.6666667
## 95 percent confidence interval:
## 0.6313501 0.7626104
## sample estimates:
## probability of success
## 0.7
无法拒绝原假设,认为随从和法术上手的几率是一样的。
尝试诸多检验之后,沮丧的发现,实际上整个实验都是与随机数做斗争,并没有足够确切的证据显示,网民所期待的那样,“炉石”背后有位“经验老道”的发牌员。

三、结论
1.单纯从直方图、概率密度图看,费用与轮次是有一定关系的,但仅在放宽犯错误的概率的情况下,卡方检验能得到先后次序会影响上手费用,但整体上看费用出现情况比较均匀,也就是说,对照详细频数,“发牌员”趋向于给玩家更不好的卡,0、7+费实际上是玩家不太希望第一轮上手的卡,而1、2费则是玩家最希望上手的卡,根据直方图,第二轮派牌策略实际上更趋向于给不太好的卡,这是单纯用检验没有办法得到的。
2.从多个检验的失效看出,也许“炉石”背后并没有网络上谣传的“发牌员”,而发牌时所遵循的策略仅仅是生成一系列来自均匀分布的随机数罢了。但毫无疑问,在暴雪承认暗改竞技场选牌机制之后,改动抽牌概率也是极有可能的,当前在实验中发现仅有选牌轮次可能存在差异,可以提醒玩家尽量不要怀有“搏一搏”的心态
四、不足与局限
1.由于本人卡牌有限,无法更好的排列出更多的实验模型,还有潜在的一些选牌因素无法得到验证,例如:为了增加玩家对新版本的熟悉度,是否选牌与卡牌版本有关(之前有过的概率调整是将新版本卡牌在竞技场中的被选率提高)
2.无法消除由个人账号带来的影响,本人非人民币玩家,可能并不在炉石希望改善用户体验的范畴之内,所以可能没有被暗中改动
3.比较难研究交叉项带来的影响,由于法术牌最高也就到7费,而大部分高费牌卡牌稀有度比较高,这样研究交互项时,无法排除各因素之间的联系,所以仅能对单独的一些感兴趣的交互项做研究
4.炉石最吸引玩家的其实是卡牌开包机制的研究,但由于每天能靠任务赚得的包是有限的,所以无法得到大量数据,探究“开包出橙率”与“时间”、“开包姿势”、“开包玩家”、“是否是连续开包”等等更为有趣的因素。所以目前仍有很大的探索空间。
五、参考文献
1.我来决定你的牌运 炉石发牌员现身说法(http://ls.duowan.com/1606/328720305017.html)
2.第六篇:R语言数据可视化之数据分布图(直方图、密度曲线、箱线图、等高线、2D密度图)(https://www.cnblogs.com/muchen/p/5430536.html)
3.神抽or鬼抽 炉石中的发牌员真的存在吗?(http://games.sina.com.cn/o/z/hs/2016-05-23/fxsktkp9166036.shtml)
六、附录代码
dat<-read.csv("01.csv",head=T,sep=",")
###画图
dat$轮次<-as.factor(dat$轮次)
library(ggplot2)
library(easyGgplot2)
p1<-ggplot(dat,aes(x=费用))+
geom_histogram(aes(fill=轮次,y=..density..),position="dodge",alpha=0.5,colour="black",binwidth=1)+
stat_density(geom="line",position="identity",size=1.5,aes(colour=轮次))+
xlab("费用")+ylab("density")+guides(fill=FALSE)+scale_fill_discrete(name="轮次")
p2<-ggplot(dat,aes(x=稀有度))+
geom_histogram(aes(fill=轮次,y=..density..),position="dodge",alpha=0.5,colour="black",binwidth=1)+
stat_density(geom="line",position="dodge",size=1.5,aes(colour=轮次))+
xlab("稀有度")+ylab("density")+guides(fill=FALSE)+scale_fill_discrete(name="轮次")
p3<-ggplot(dat,aes(x=factor(职卡),fill=轮次))+geom_histogram(stat="count",position="dodge")+
xlab("是否是职业卡")+ylab("频率")+scale_fill_discrete(name="轮次")
p4<-ggplot(dat,aes(x=factor(法随),fill=轮次))+geom_histogram(stat="count",position="dodge")+
xlab("是法术或随从")+ylab("频率")+scale_fill_discrete(name="轮次")
ggplot2.multiplot(p1,p2,p3,p4,cols=2)
###各种检验
test<-c(table(dat$稀有度))
real<-c(8,8,7,7)*200/30
testdat<-matrix(c(test,real),byrow=F,,2)
chisq.test(testdat)
test<-c(table(dat$费用))
real<-rep(1,10)*20
testdat<-matrix(c(test,real),byrow=T,2)
chisq.test(testdat)
first<-table(dat[dat$轮次==1,]$费用)
second<-table(dat[dat$轮次==2,]$费用)
chisq.test(first,second)
d<-dat[dat$稀有度==3,]
d<-d[d$费用<3,]
binom.test(length(d[,1]),200,1/30)
binom.test(sum(dat$法随),200,2/3)
chisq.test(x=table(dat$费用))
xx<-table(dat[dat$轮次==1,]$费用)
yy<-table(dat[dat$轮次==2,]$费用)
###观察详情
plot(x=1:9,y=seq(4,16,6/5),type="n")
lines(xx,type="l",col="black")
lines(yy,type="l",col="blue")
lines(rep(10,10),type="l",col="red")
lines(xx-yy,type="l")